Elm Queues Shootout!

Today’s story begins in the Elm Slack, where I saw a RSS integration post a notification about a new package:

I do love PBT-testing data container libraries against the “spec” when given the opportunity, and since I created myself a small tool called elm-bench for easier benchmarking, I couldn’t resist and decided to find all the queue packages currently available on package.elm-lang.org and put them under the microscope. Let’s thoroughly test and benchmark them!

The rest of this blogpost shows the results of my testing and benchmarking, and I will attempt to categorize the packages and recommend the best ones.

Spoiler alert: I did find a bug, though not in the new library that started the whole effort!

Packages

Here’s what we’ll be testing:

Note I have excluded francescortiz/elm-queue from the comparison because it deals with rate limiting, keyed values etc. and is not as general-purpose as the others. One could create a generic queue out of it but it would have severe overhead (2+ orders of magnitude).

On the other hand, I am including deques (double-ended queues) in the comparison.

Expected API: what is a Queue?

Queues are relatively simple: they’re a container holding 0+ items, and you can efficiently push (enqueue) an item on one side and pop (dequeue) an item on the other side (first in, first out).

Let’s expect the some variation on the following API from all of these packages:

type Queue a
empty : Queue a
isEmpty : Queue a -> Bool
singleton : a -> Queue a
fromList : List a -> Queue a
toList : Queue a -> List a
enqueue : a -> Queue a -> Queue a
dequeue : Queue a -> Maybe (a, Queue a)
length : Queue a -> Int

For length, if the package doesn’t give us an “official” way, we have two options on how to implement it: via toList and via repeated calls to dequeue (or perhaps fold, if provided). The performance difference could swing both ways, so let’s create both and measure instead!

API differences

All of the packages indeed allow us to express the above API.

Here is a comparison of which functions are provided out of the box:

function	`avh4`	`dwayne`	`folkertdev`	`kudzu-forest`	`owanturist`	`robinheghan`	`turboMaCk`
empty	✅	✅	✅	✅	✅	✅	✅
isEmpty	❌	✅	✅	❌	✅	✅	✅
singleton	❌	❌	✅	❌	✅	✅	✅
fromList	✅	✅	✅	✅	✅	✅	✅
toList	✅	✅	✅	✅	✅	✅	✅
enqueue	✅	✅	✅	✅	✅	✅	✅
dequeue	✅	✅	✅	✅	✅	✅	✅
length	❌	❌	✅	✅	✅	✅	✅

Other exposed functions:

dwayne/elm-queue (1)
- peek
folkertdev/elm-deque (11+5)
- append, member, first, takeFront, map, map2, andMap, filter, foldl, partition, isEqualTo
- deque-specific: pushBack, popFront, last, takeBack, foldr
kudzu-forest/elm-constant-time-queue (6)
- head, map, fold, isEqual, fromListLIFO, toListFIFO
owanturist/elm-queue (34)
- repeat, range, head, tail, take, drop, partition, unzip, any, all, member, maximum, minimum, sum, product, map, indexedMap, foldl, foldr, filter, filterMap, reverse, append, concat, concatMap, intersperse, map2, map3, map4, map5, sort, sortBy, sortWith, equals
robinheghan/elm-deque (15+4)
- initialize, repeat, range, append, left, right, dropLeft, dropRight, member, first, map, filter, filterMap, foldl, partition
- deque-specific: pushBack, popFront, last, foldr
turboMaCk/queue (5)
- front, dropFront, map, filter, updateFront

Equality gotcha

Note that using the built-in Elm == equality operator on queues is unsafe for ALL of these packages, as some values can have multiple internal representations. The canonical example is Chris Okasaki’s queue design with two lists, one for the rear and one for front. You could imagine two queues for singleton 1: Q [1] [] and Q [] [1], and so on.

When working with Queue packages you need to use their provided equality predicates, or use toList to find out if two queues contain the same values in the same order.

Expected invariants

Here are the properties I believe should hold for any queue. Properties having ∀ (“for all”) qualifiers can be checked using property-based tests, properties not having them can be checked using unit tests.

Note that many of these will overlap; I’ve just found it easiest to find properties by looking at pairs of functions.

The == operator below is to represent the correct way to compare two queues for equality (see note above).

Here’s the types of the variables introduced in the for-alls:

x : a
xs : List a
q : Queue a -- created via fromList

The invariants we will be checking:

empty / isEmpty
- isEmpty empty == True
empty / singleton / enqueue
- ∀x: enqueue x empty == singleton x
empty / singleton / dequeue
- ∀x: dequeue (singleton x) == Just (x, empty)
empty / fromList
- empty == fromList []
empty / toList
- toList empty == []
empty / dequeue
- dequeue empty == Nothing
empty / length
- length empty == 0
isEmpty / singleton
- ∀x: isEmpty (singleton x) == False
isEmpty / fromList
- ∀xs: isEmpty (fromList xs) == List.isEmpty xs
isEmpty / toList
- ∀q: isEmpty q == List.isEmpty (toList x)
isEmpty / length
- ∀q: isEmpty q == (length q == 0)
singleton / fromList
- ∀x: singleton x == fromList [x]
singleton / toList
- ∀x: toList (singleton x) == [x]
singleton / length
- ∀x: length (singleton x) == 1
fromList / toList
- ∀xs: toList (fromList (xs)) == xs
fromList / enqueue
- ∀x,xs: enqueue x (fromList xs) == fromList (xs ++ [x])
fromList / length
- ∀xs: length (fromList xs) == List.length xs
toList / enqueue
- ∀x,q: toList (enqueue x q) == toList q ++ [x]
toList / length
- ∀q: length q == List.length (toList q)
enqueue / length
- ∀x,q: length (enqueue x q) == 1 + length q
length
- ∀q: lengthViaToList q == lengthOriginal q (where applicable)
- ∀q: lengthViaDequeue q == lengthOriginal q (where applicable)
- ∀q: lengthViaToList q == lengthViaDequeue q

Invariant differences / bugs found

All tested packages behaved identically and as-expected, with the exception of owanturist/elm-queue.

This library behaves differently wrt. fromList and toList: compared to other libraries, they act as if they reversed the list in question:

dequeue (fromList [1,2,3])
-- owanturist/elm-queue:
Just (3, queueWithout3)
-- others:
Just (1, queueWithout1)

toList (enqueue 999 (singleton 1))
-- owanturist/elm-queue:
[999,1]
-- others:
[1,999]

Taken together, the two bugs cancel out (ie. the roundabout test “fromList / toList” doesn’t catch them), which makes them sneakier in retrospect.

This was submitted to the package repository as issue #5.

Performance

I’m using elm-bench to write these benchmarks. It’s a tool I wrote to reduce boilerplate when using the de-facto Elm benchmarking library, elm-explorations/benchmark.

Benchmarks were ran on a Macbook Pro (16-inch, Nov 2024) with the Apple M4 Pro CPU and 48 GB RAM; Node v22.16.0 and Elm 0.19.1.

My setup is the following:

.
├── v01_avh4
│   ├── elm.json
│   ├── src
│   │   └── CommonApi.elm
│   └── tests
│       └── QueueInvariants.elm
├── v02_dwayne
│   ├── elm.json
│   ├── src
│   │   └── CommonApi.elm
│   └── tests
│       └── QueueInvariants.elm
├── v03_folkertdev
│   ├── elm.json
│   ├── src
│   │   └── CommonApi.elm
│   └── tests
│       └── QueueInvariants.elm
├── v04_kudzu-forest
│   ├── elm.json
│   ├── src
│   │   └── CommonApi.elm
│   └── tests
│       └── QueueInvariants.elm
├── v05_owanturist
│   ├── elm.json
│   ├── src
│   │   └── CommonApi.elm
│   └── tests
│       └── QueueInvariants.elm
├── v06_robinheghan
│   ├── elm.json
│   ├── src
│   │   └── CommonApi.elm
│   └── tests
│       └── QueueInvariants.elm
└── v07_turboMaCk
    ├── elm.json
    ├── src
    │   └── CommonApi.elm
    └── tests
        └── QueueInvariants.elm

Each of the CommonApi.elm files contains an implementation of the, well, common API.

The implementations (and tests) for each tested package can be found in the accompanying repository: Janiczek/elm-queues-shootout.

I then run the benchmarks via elm-bench in the “version” mode: this allows me to have a separate project for each library. I can’t use them all in the same Elm project because of module name collisions: many of the packages export a module named Queue, and there can only be one.

alias bench_queues="elm-bench --json -v v01_avh4 -v v02_dwayne -v v03_folkertdev -v v04_kudzu-forest -v v05_owanturist -v v06_robinheghan -v v07_turboMaCk"

Example usage:

bench_queues CommonApi.dequeue "(CommonApi.fromList (List.range 1 5))"
bench_queues CommonApi.enqueue 1 CommonApi.empty

elm-bench ensures the arguments to the function are precomputed (by putting them in their own top-level declarations, which are then computed during program initialization and before the benchmark starts). This means we aren’t measuring the runtime of computing the arguments.

The --json flag gives output in a JSON form, from which the measurement can be plucked via jq ".[].nsPerRun". All measurements are in nanoseconds per run (that is, per the measured function call).

Finally, “small queue/list” means List.range 1 5 and “Large queue/list” means List.range 1 500.

Measurements

I need to preface this with: this is all on a nanosecond scale. Don’t be wooed by the absolute differences here - does your webapp really care about 0.2ns vs 3ns? Which operations will it do often? The O(1) vs O(N) time complexities will probably be more instructive, though again you have to think about the realistic sizes of your queues. Are they going to hold more than a few hundred items?

The table with the measurements is on Github, my blog CSS is simply not up to such a gargantuan task and I can’t be bothered to tweak it right now. CSV is more usable than a HTML table anyways!

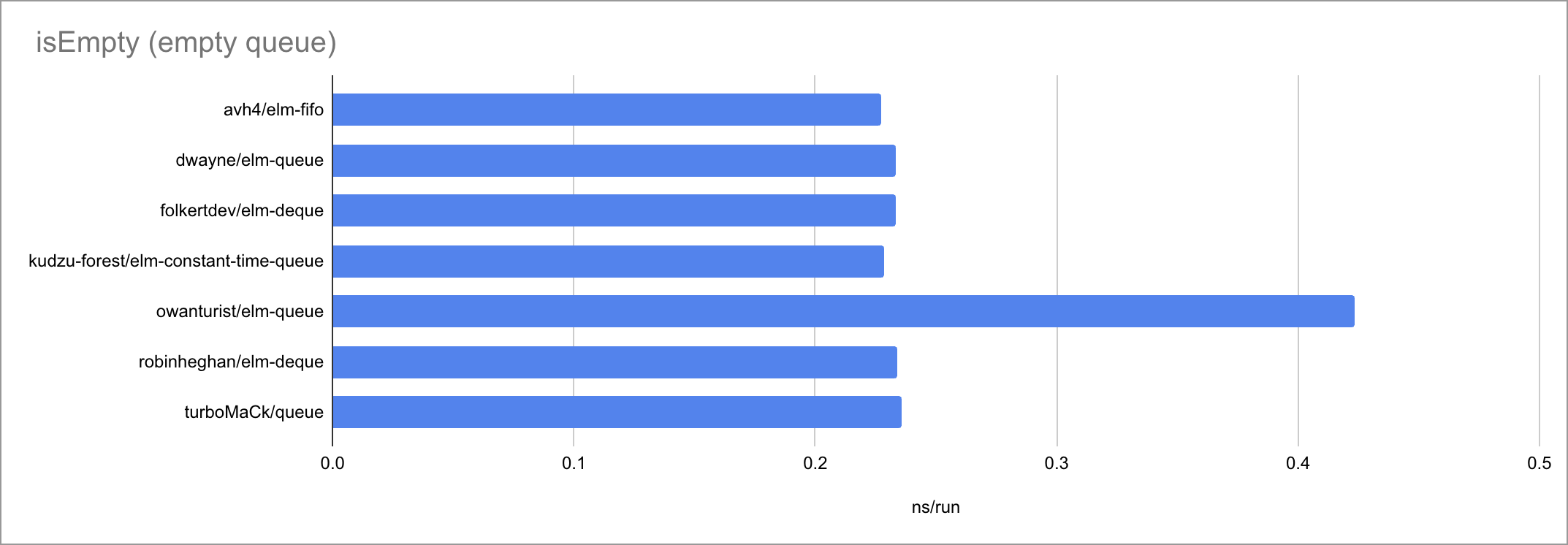
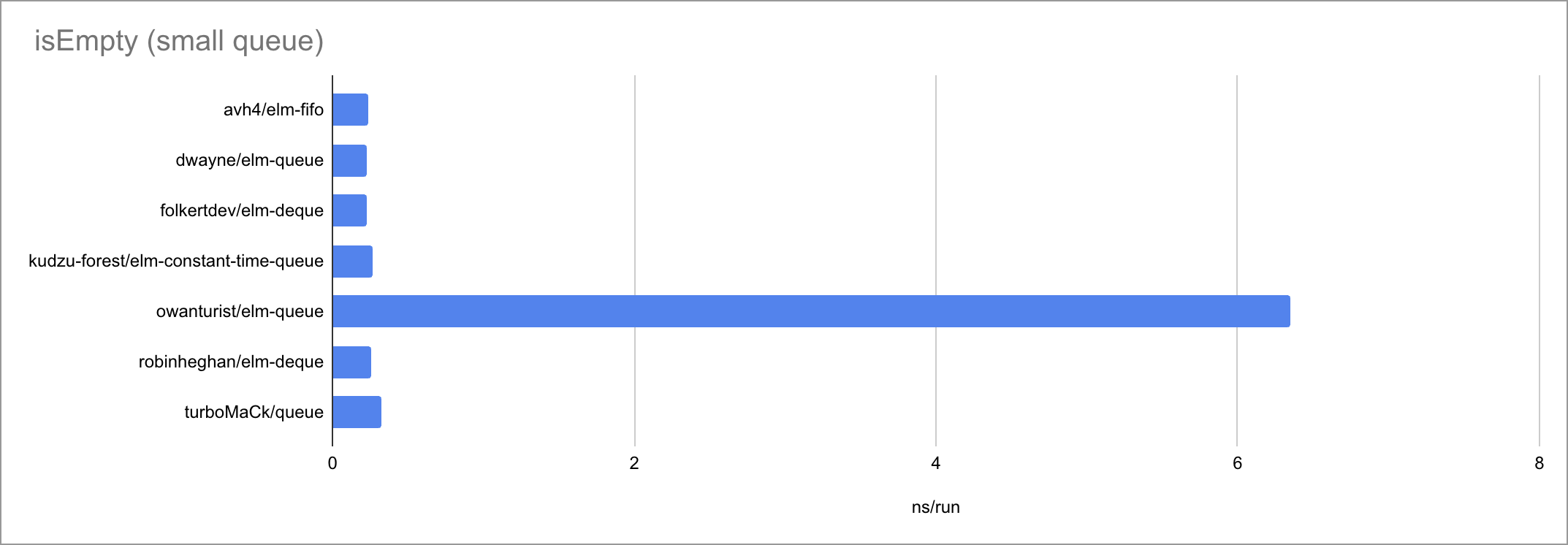
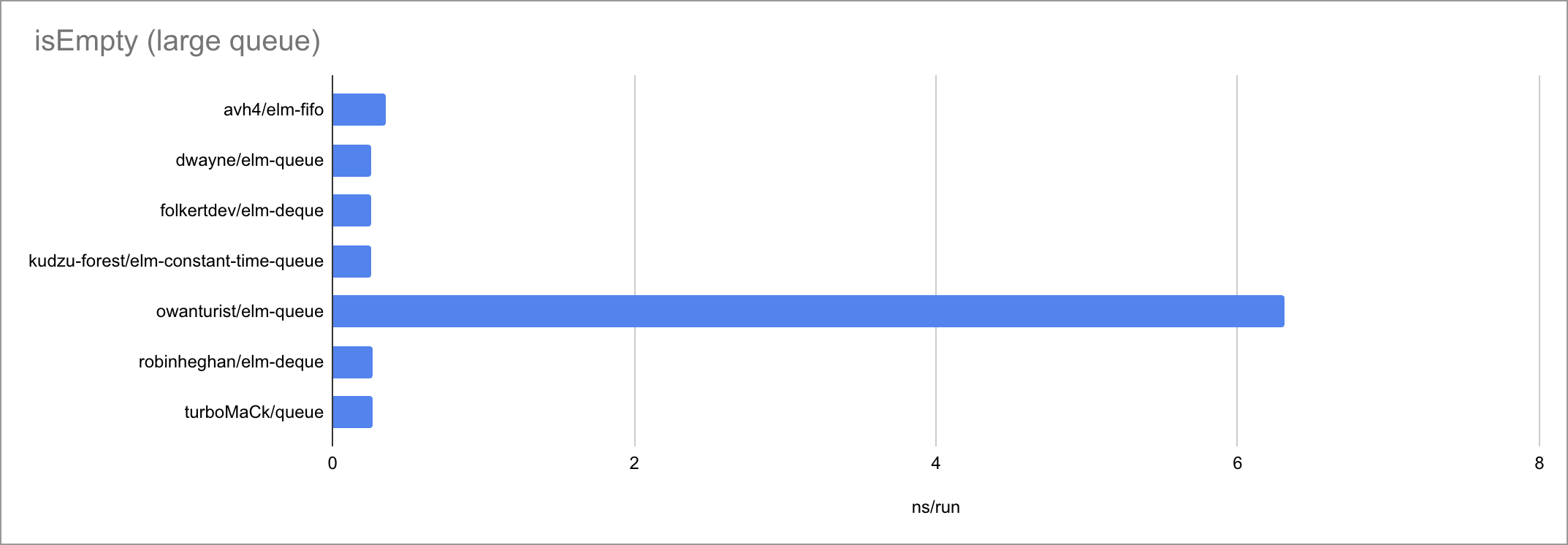
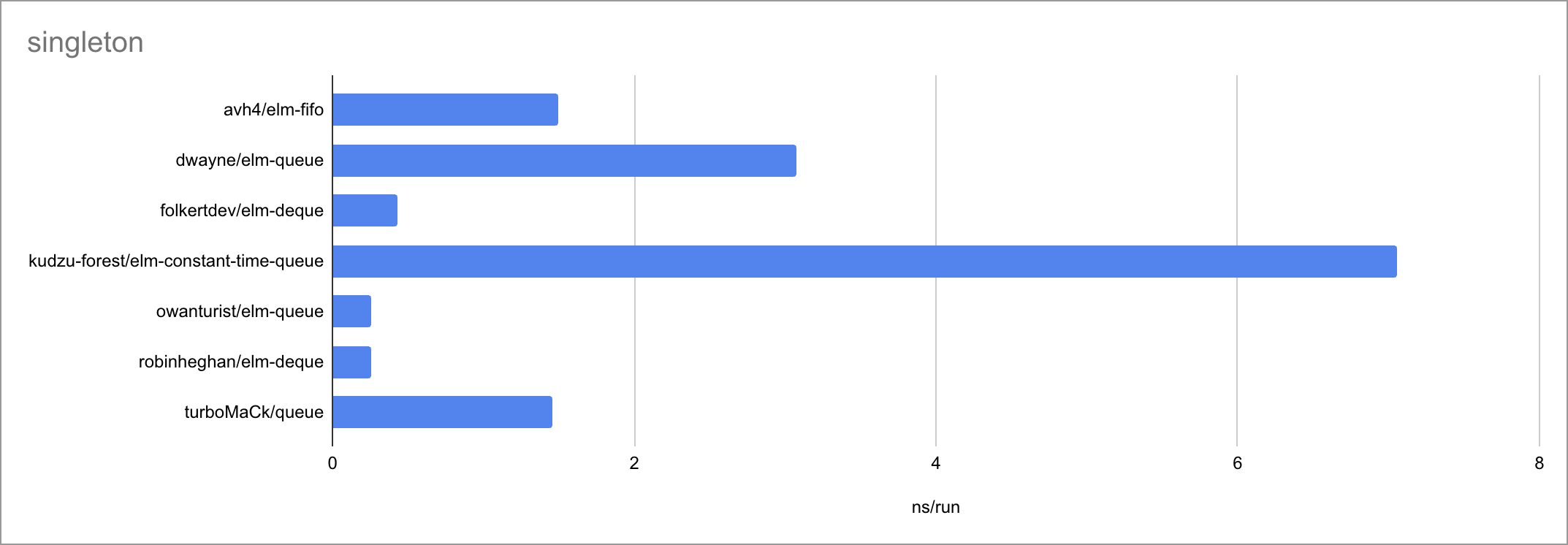
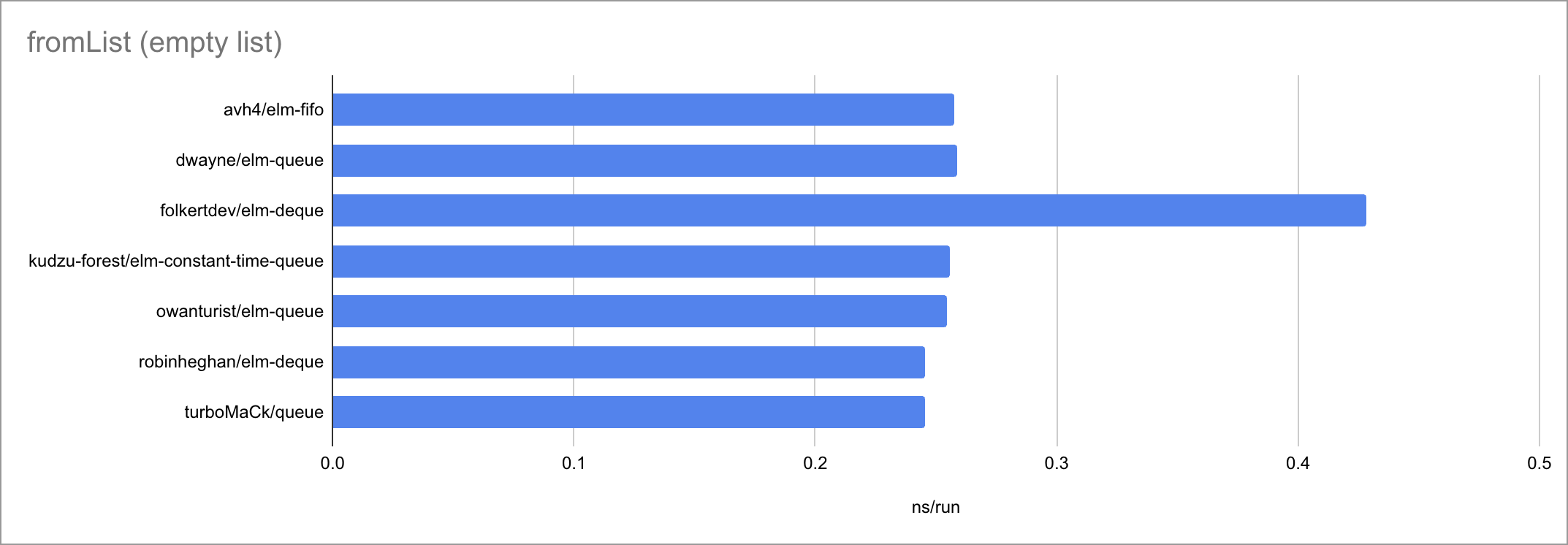
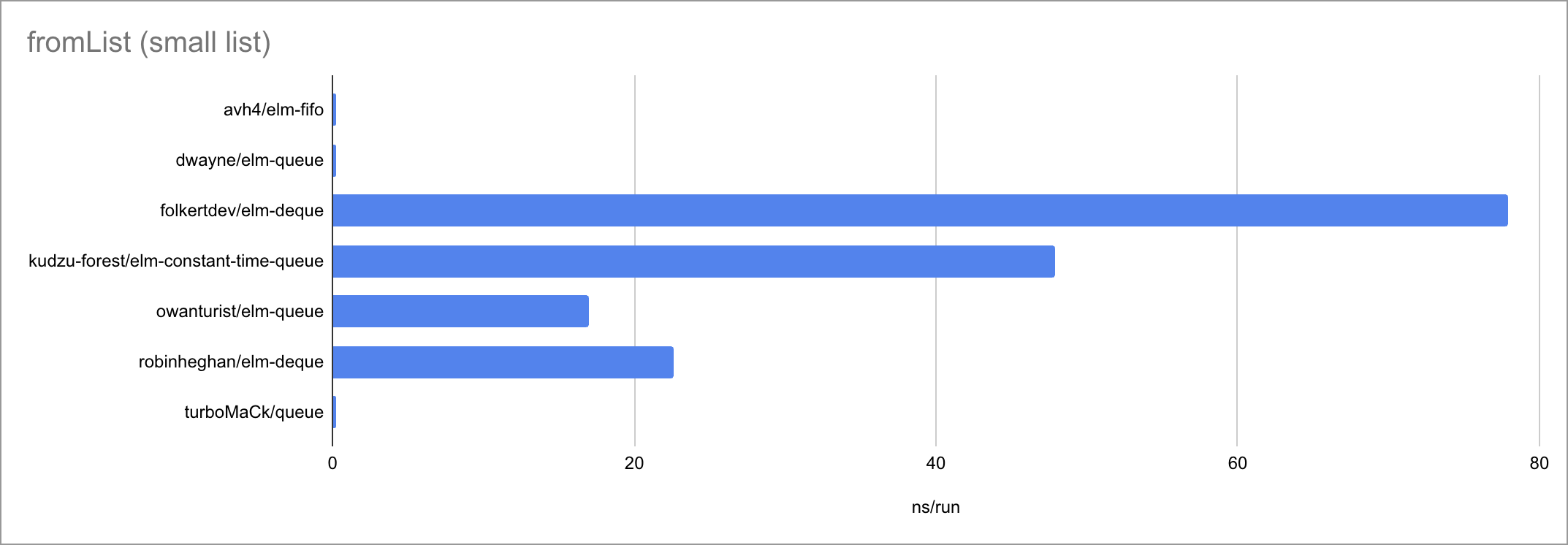
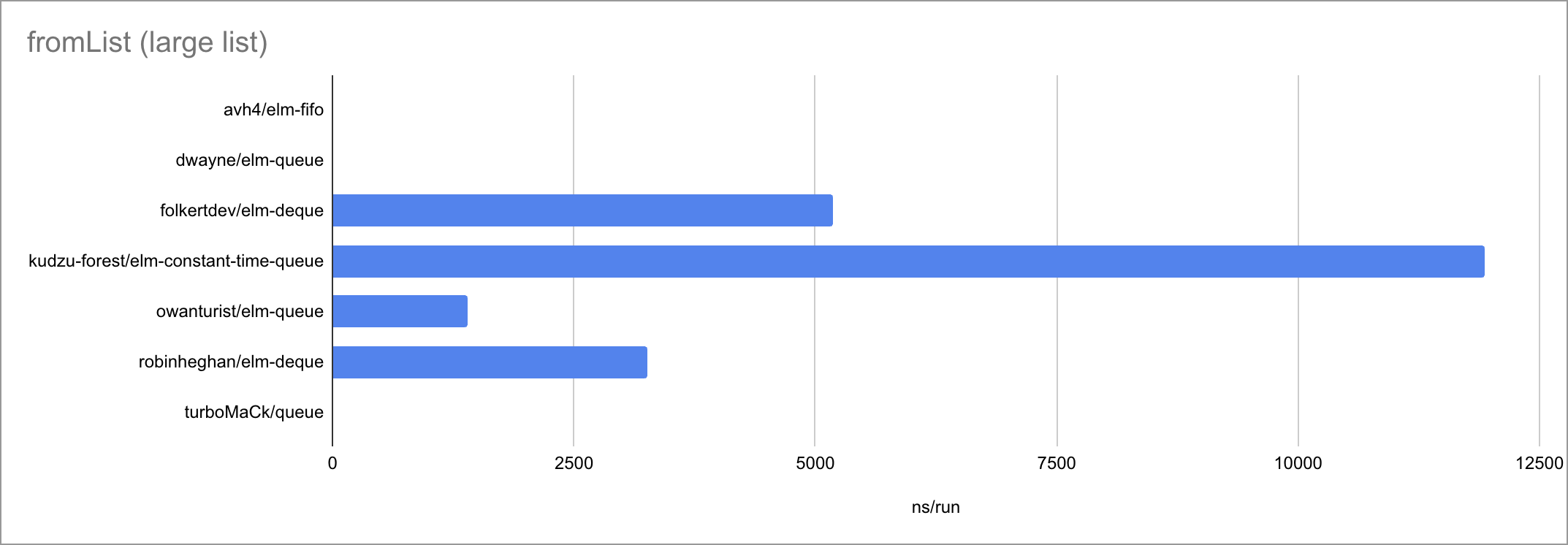
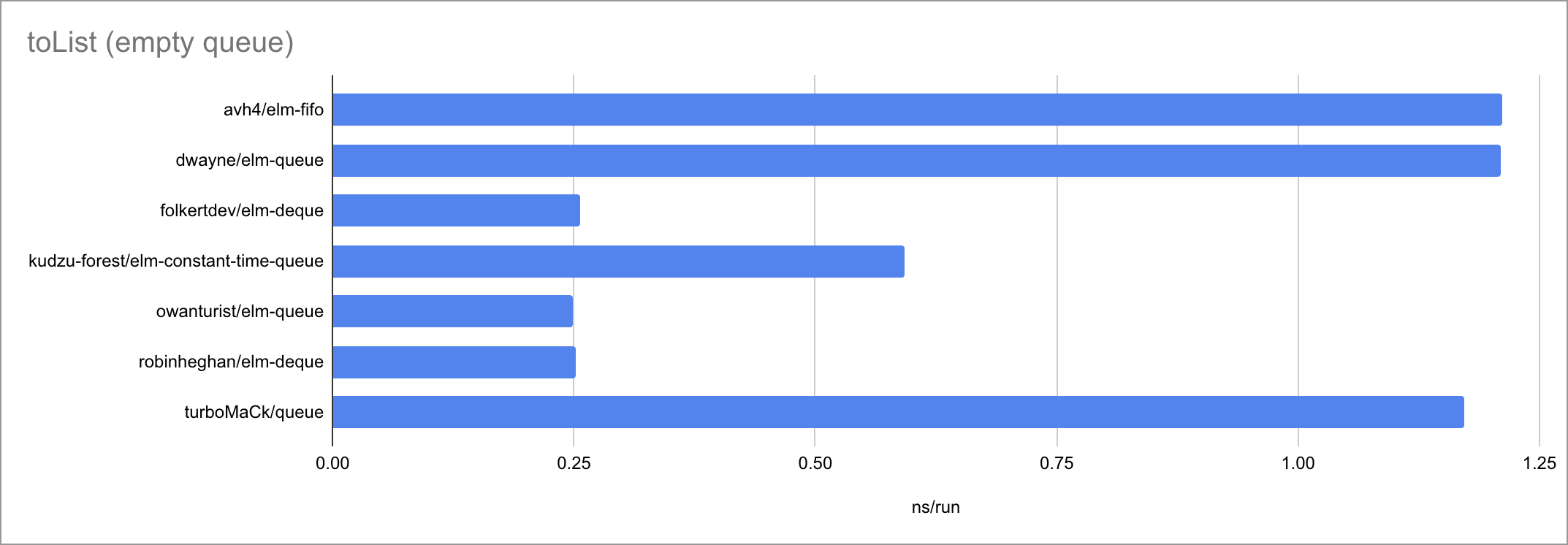
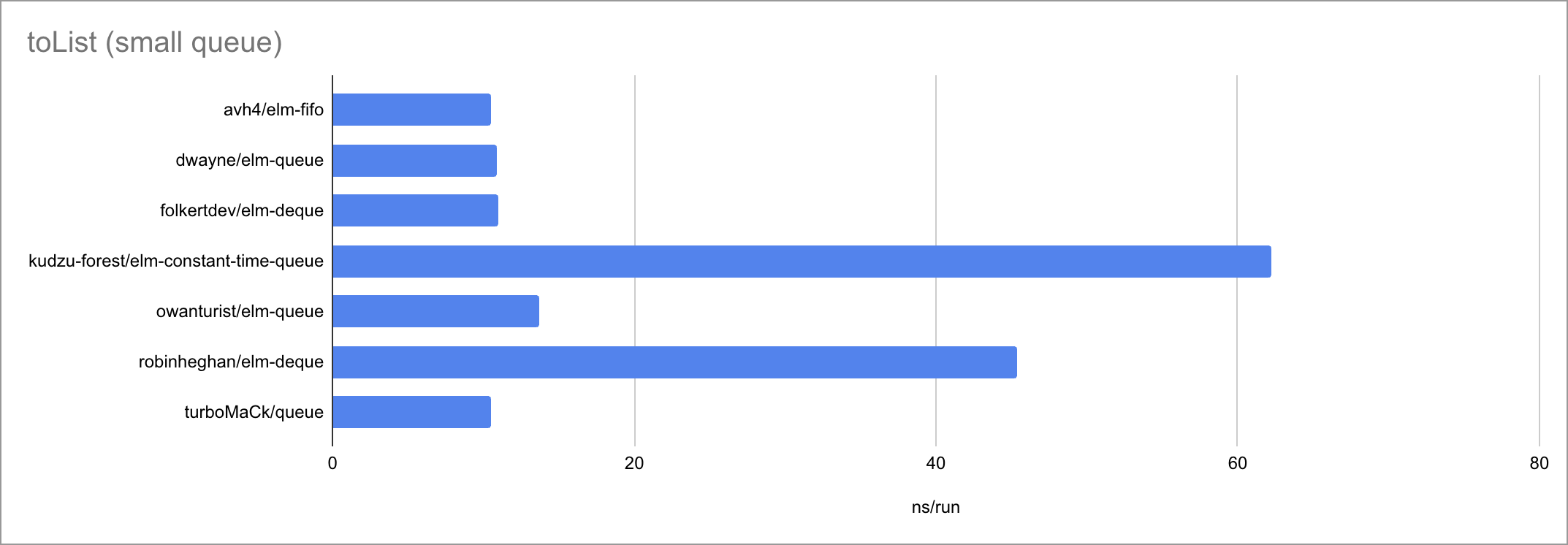
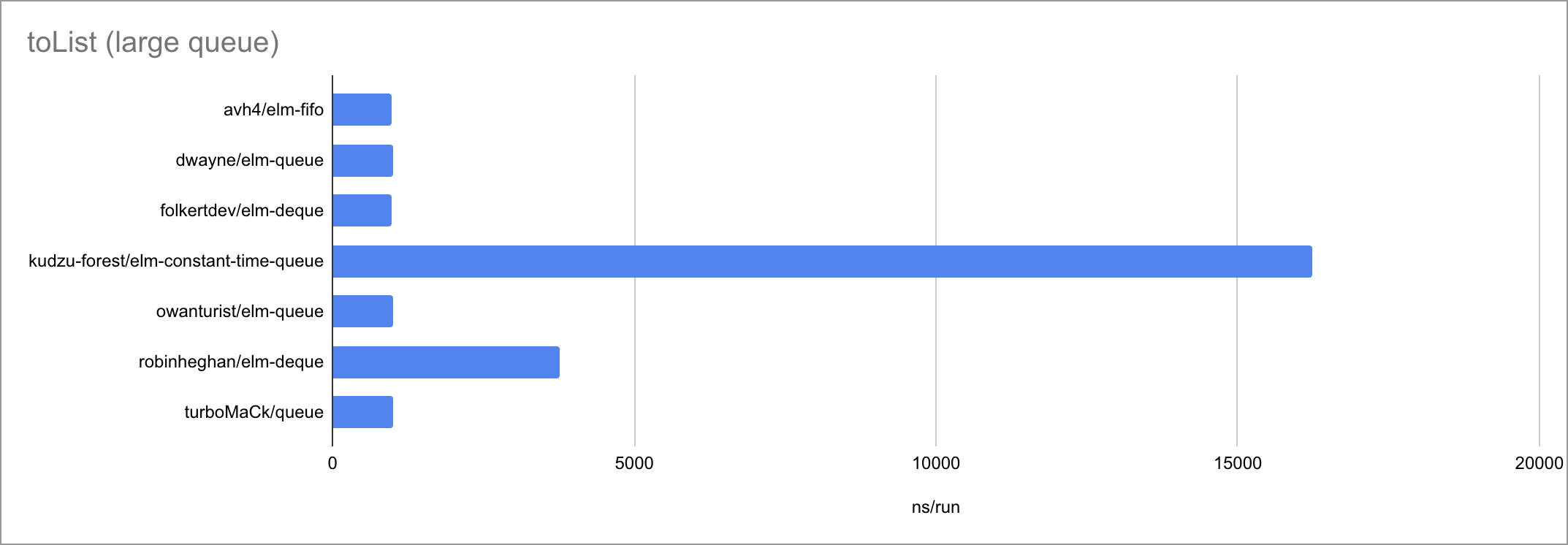
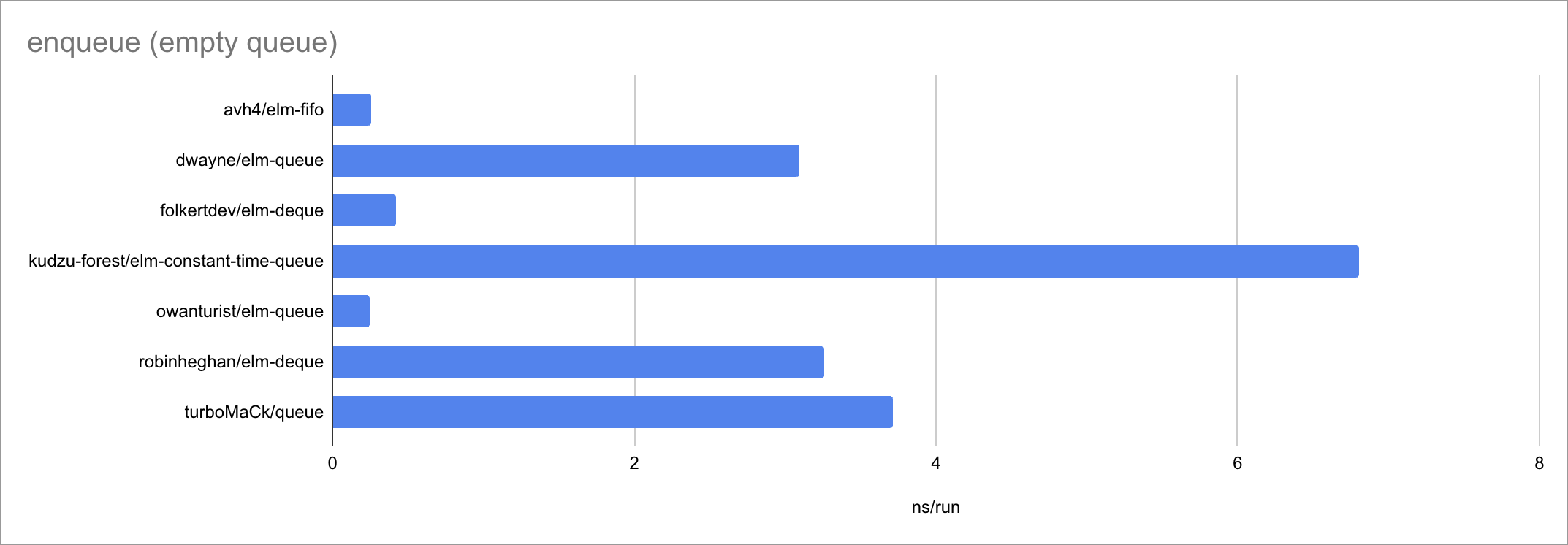
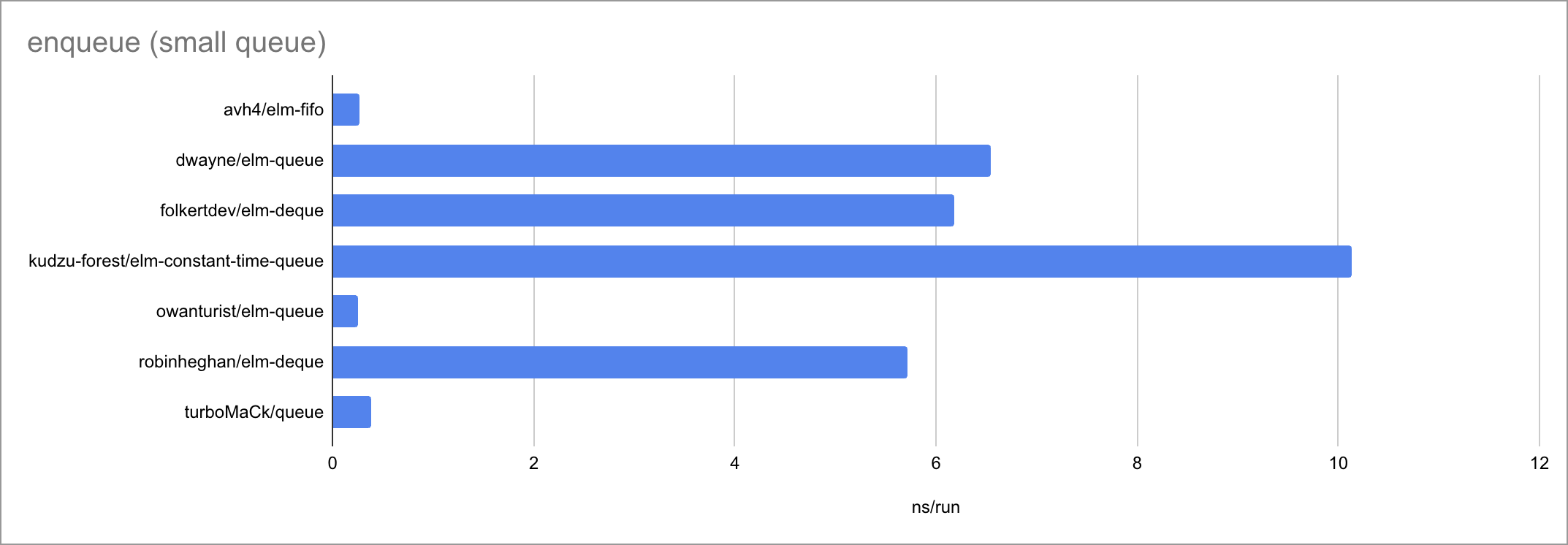
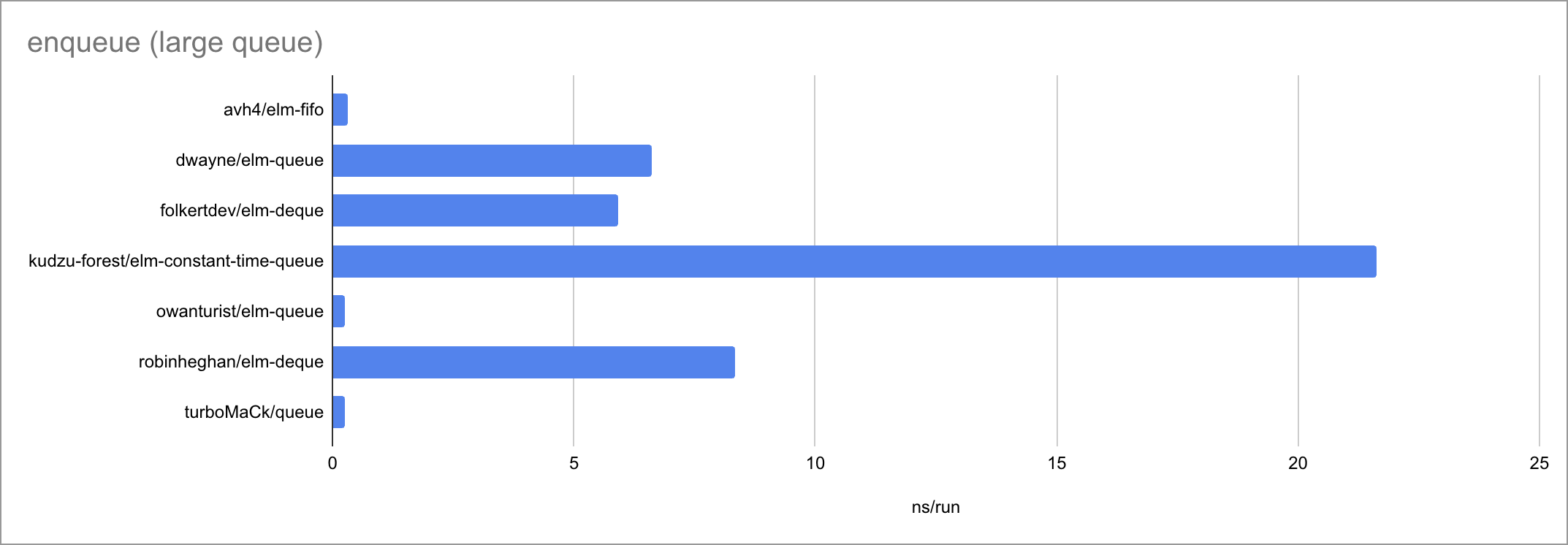
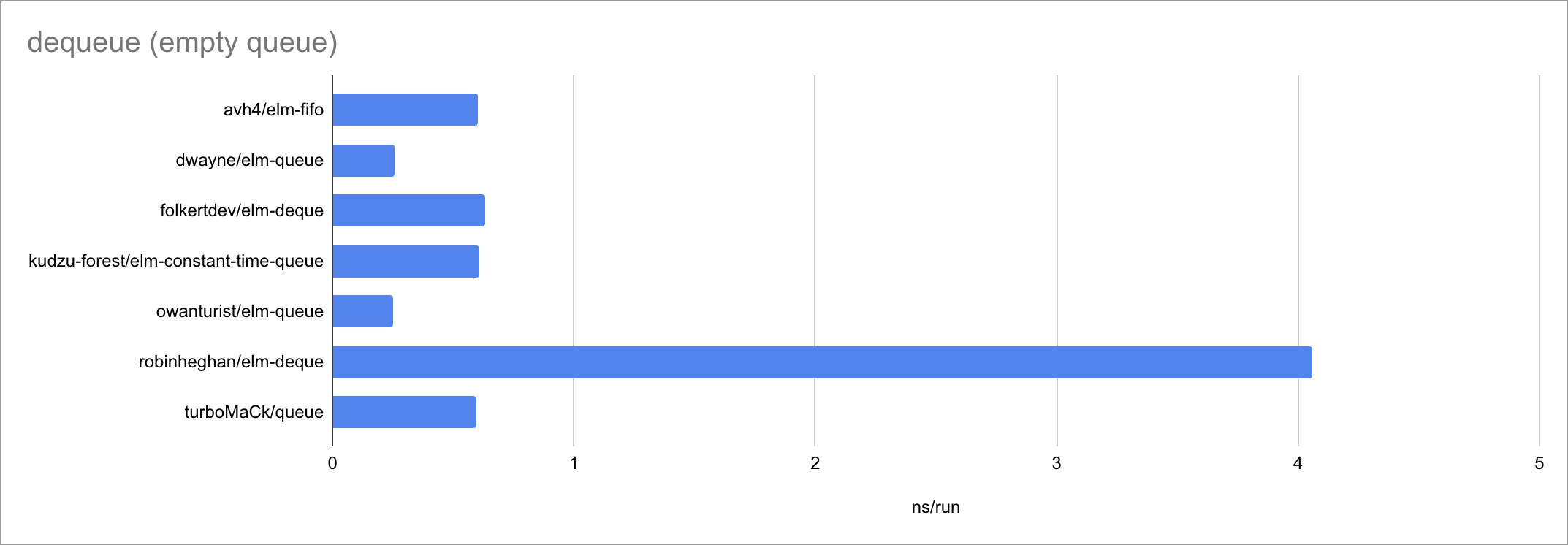
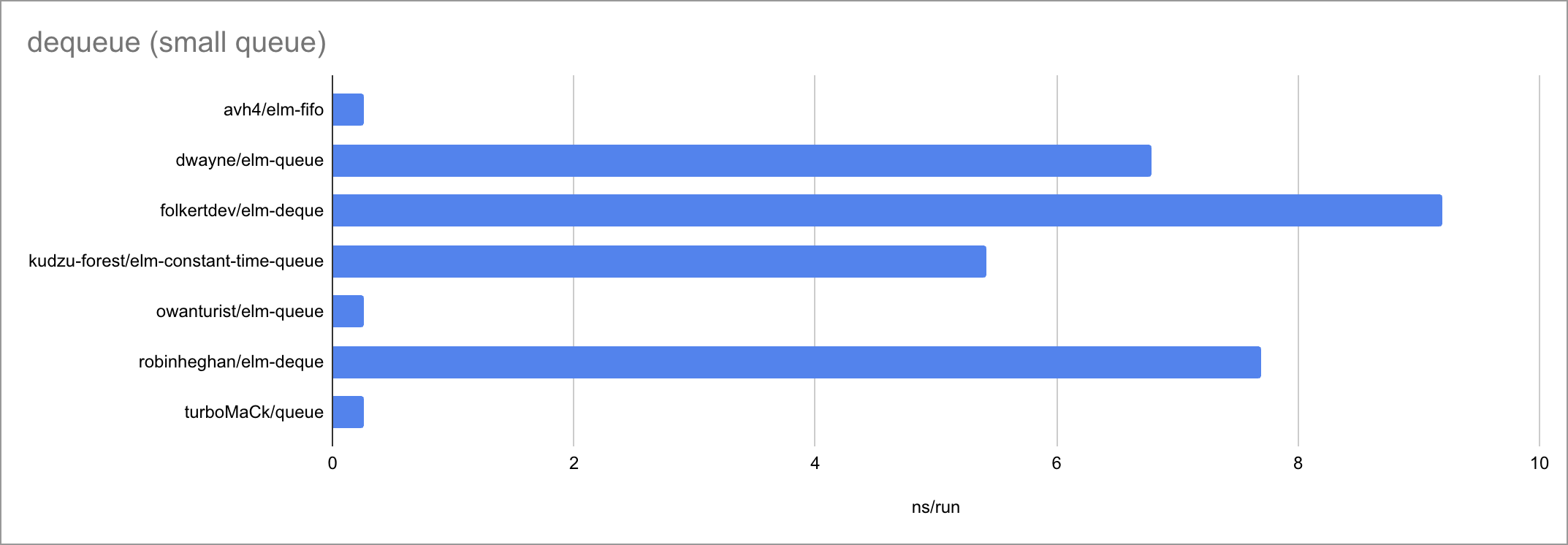
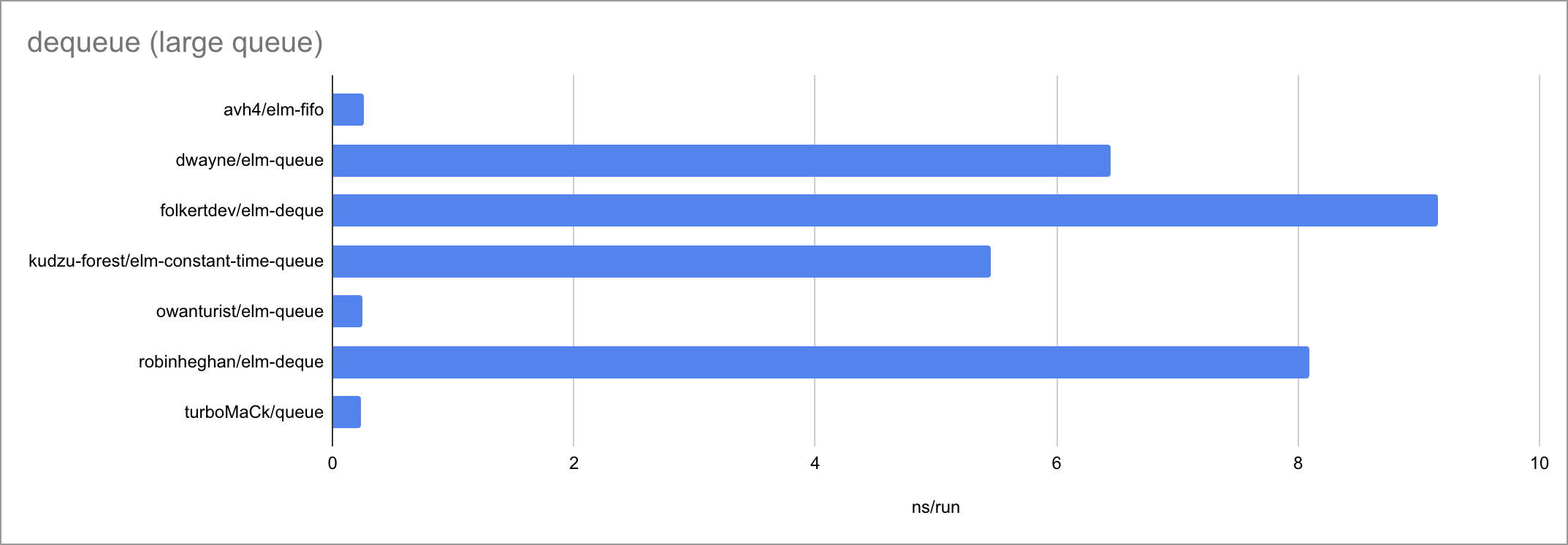
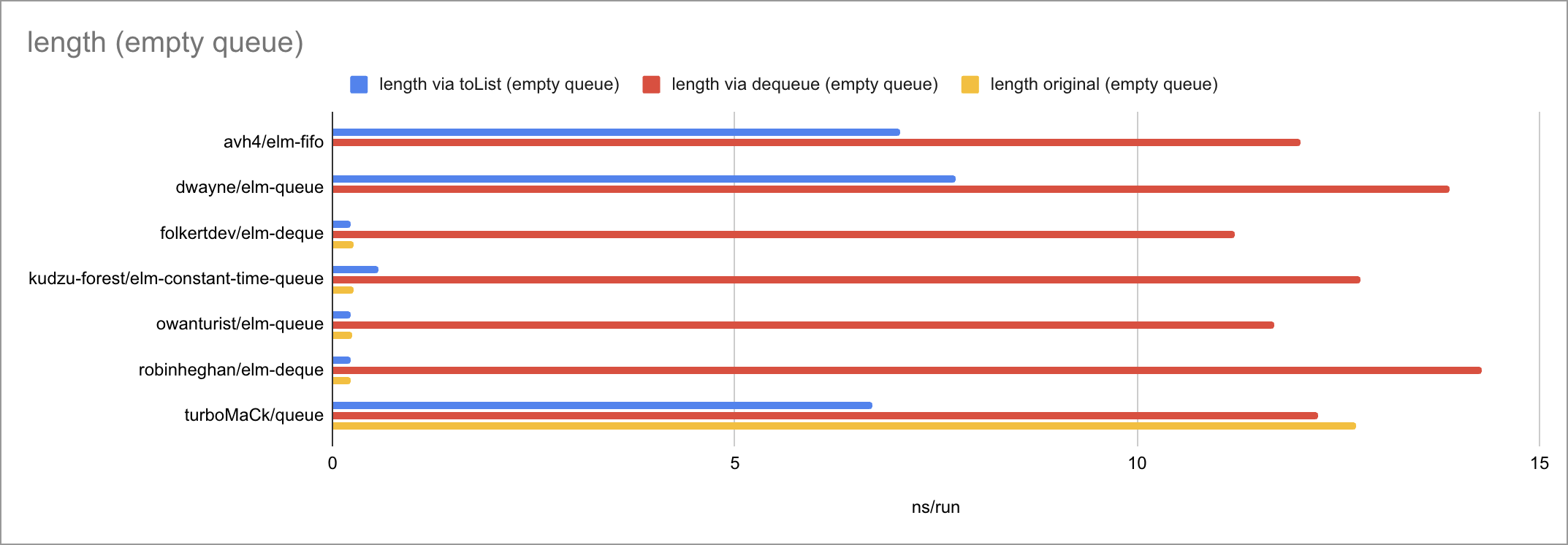
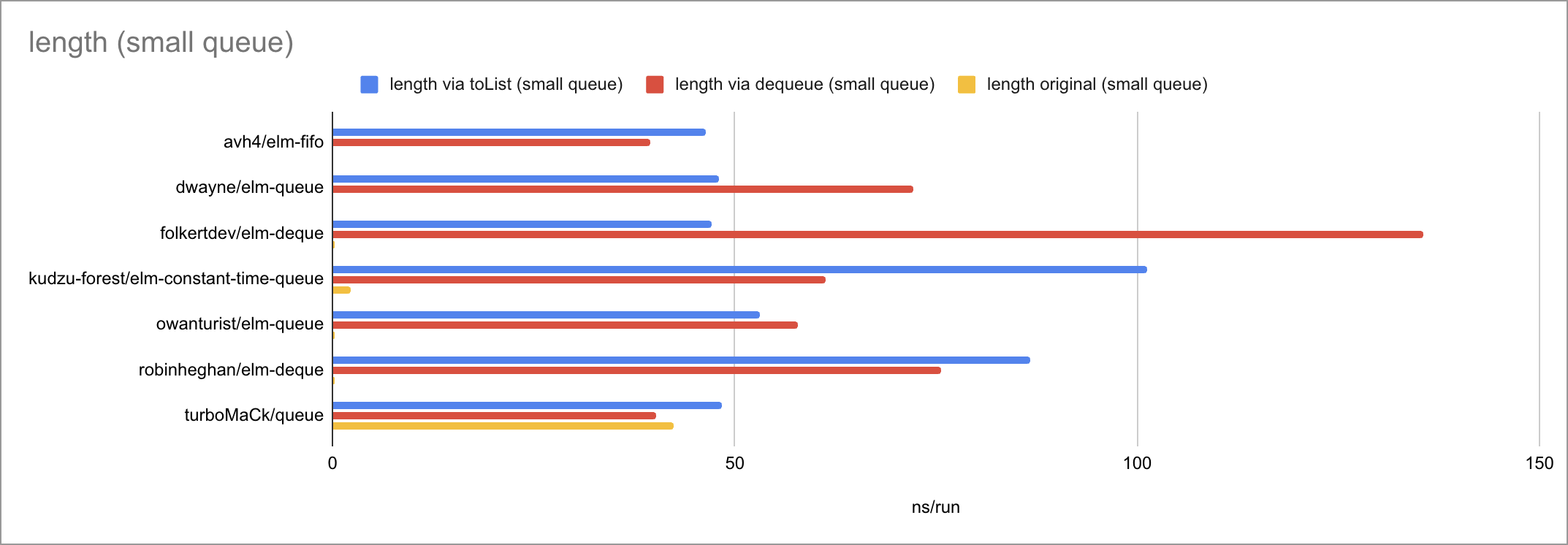
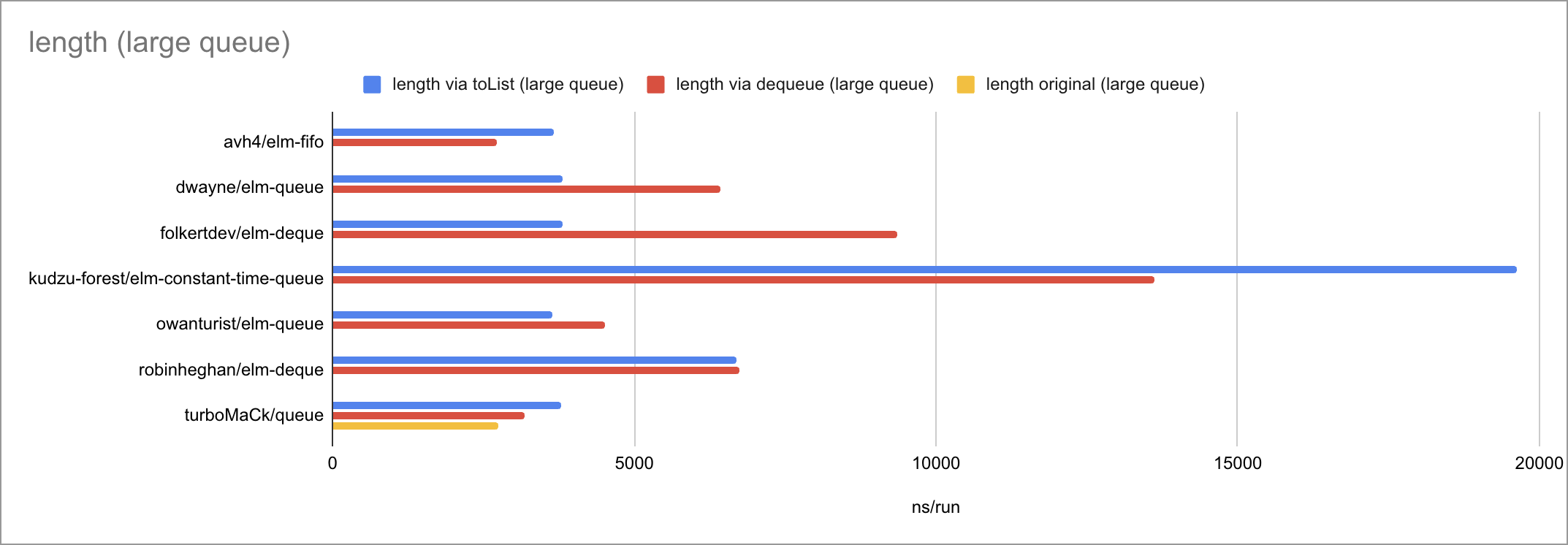
Some charts (as always, click to zoom):

Based on the limited amount of datapoints (lengths of the input list or queue), I believe we can jot down these time complexities:

test	`avh4`	`dwayne`	`folkertdev`	`kudzu-forest`	`owanturist`	`robinheghan`	`turboMaCk`
isEmpty	O(1)	O(1)	O(1)	O(1)	O(1)	O(1)	O(1)
singleton	O(1)	O(1)	O(1)	O(1)	O(1)	O(1)	O(1)
fromList	O(1)	O(1)	O(N)	O(N)	O(N) 🐛	O(N)	O(1)
toList	O(N)	O(N)	O(N)	O(N)	O(N) 🐛	O(N)	O(N)
enqueue	O(1)	O(1)	O(1)	O(logN)?	O(1)	O(logN)?	O(1)
dequeue	O(1)	O(1)	O(1)	O(1)	O(1)	O(1)	O(1)
length	-	-	O(1)	O(logN)	O(1)	O(1)	O(N)

It’s fascinating to see how at such small timescales, every little function call, if expression and pattern match matters. There is a very visible bimodality: the empty case behaves very differently from the two measured non-empty cases, taking a different path through the code. Sometimes surprisingly for the worse!

When a library implements length, it’s usually way better (in most cases, O(1)) than anything you can implement yourself from toList or dequeue (where you’re guaranteed O(N)).

And yet again, it’s hard to say how much will a hypothetical webapp feel any of this. We’re on the scale of nanoseconds, basically almost none of this matters unless you’re doing this in a hot loop or on huge datasets!

length / fromList tradeoff

There is an inevitable tradeoff between O(1) length + O(N) fromList and O(N) length + O(1) fromList, as the native Elm lists don’t hold length metadata and thus have O(N) length themselves.

This means that to hold the precomputed number of elements in the queue implementation (O(1) length), you need to count the elements during insertion: O(N) fromList.

If you instead want to just hold the list the user gave you, without walking it (possibly O(1) fromList), you’ll have to walk it in length to count the elements (O(N) length).

You have to count the elements somewhere: on the way in or on the way out.

Categorization

It seems that there are two categories you can choose from:

Deques with somewhat rich List-like API, O(1) length and O(N) fromList
- Both folkertdev/elm-deque and robinheghan/elm-deque fit the bill.
- Robin’s library seems faster at fromList and slower at toList.
- Robin also mentions possible performance differences in his README, though I haven’t tested and measured these.
Queues based on Chris Okasaki’s “two lists” design, with O(1) fromList and O(N) length
- avh4/elm-fifo, dwayne/elm-queue and turboMaCk/queue belong here.
- There are almost no differences. Dwayne’s library seems a bit slower on enqueue and dequeue than the other two. One might prefer turboMaCk’s library to avh4’s due to slightly richer API.
- A future (version of a) library could differentiate itself here by implementing a rich List-like API.

owanturist/elm-queue does have the richest API out of all the tested packages, would otherwise belong with the other three Okasaki queues and would be my recommended choice (if you don’t need a deque), but contains the buggy/surprising fromList and toList behaviour.

I’m not completely sure where to put kudzu-forest/elm-constant-time-queue. The constant-time promise for enqueue doesn’t seem to be there and the code needed for worst-time guarantees is making this library slower overall, though note that my code benchmarked one specific way of constructing a queue, and perhaps queues that are used in a more mixed way (enqueue, dequeue, enqueue again) would be more stable compared to other packages?

Summary

We found a bug in one of the libraries!

If you need a deque, choose between folkertdev/elm-deque and robinheghan/elm-deque based on the needed API or whether you’ll use fromList or toList more often.

If you just need a queue, I recommend turboMaCk/queue solely based on having slightly richer API to avh4/elm-fifo.

And if you’re one of the authors of the above libraries, adding more helper functions would help and would make you my immediate favorite :)

HP M479 unofficial cartridge

Martin Janiczek