I’ve solved a fair amount of Advent of Code puzzles in Elm, and stumbled upon a pattern that quickly became my go-to for problems like pathfinding and (mathematical) optimization.
About a week or two ago, I’ve started working on a refactoring of our core data structure from graph to a tree at Vendr, and found the pattern helpful in this domain as well.
This made me realize it might be more general and useful than I originally thought, and so I want to clarify my understanding of it by writing about it. I hope it will be helpful to you as well!
The pattern
In short, the pattern is to hold an explicit list of TODOs and then make a function handle them one by one, possibly stopping early and/or adding new TODOs to the list.
The general shape looks like this:
type alias Input = ...
type alias Output = ...
type alias Todo = ...
process : Input -> Output
process input =
let
go : List Todo -> Output
go todos =
case todos of
[] ->
-- all TODOs finished - return something
...
todo :: rest ->
if somePredicate todo then
-- possibly end instead of recursing
-- (eg. in search problems)
...
else
let
addedTodos : List Todo
addedTodos = ... -- derived from `todo`
in
-- remember the new TODOs and recurse!
go (rest ++ addedTodos) -- queue, breadth-first
-- or:
-- go (addedTodos ++ rest) -- stack, depth-first
in
go (initTodos input)
You can see it uses tail-call recursion (the inner function go returns either a value or a call to itself) and holds a list of TODOs to process. There are a few possible variations:
- Do you want depth-first traversal or breadth-first traversal?
- Do you need to process all items and collect some result value, or are you looking to find something and finish early?
- Do you need to hold some state on the side (eg. a set of visited items to not duplicate work)?
- Can you take advantage of a priority queue in place of a List?
Processing all TODOs
Below is a full example, showing off the “process all items” variation. We’ll be processing a custom tree type and listing all the a values along with paths to find them. (This is the example from my day-to-day work that prompted this blogpost!)
type Job a
= Leaf a
| Sequence (List (Job a))
| Parallel (List (Job a))
| Condition a
{ trueSeq : List (Job a)
, falseSeq : List (Job a)
}
type Step
= InSequence Int
| InParallel Int
| InCondTrue Int
| InCondFalse Int
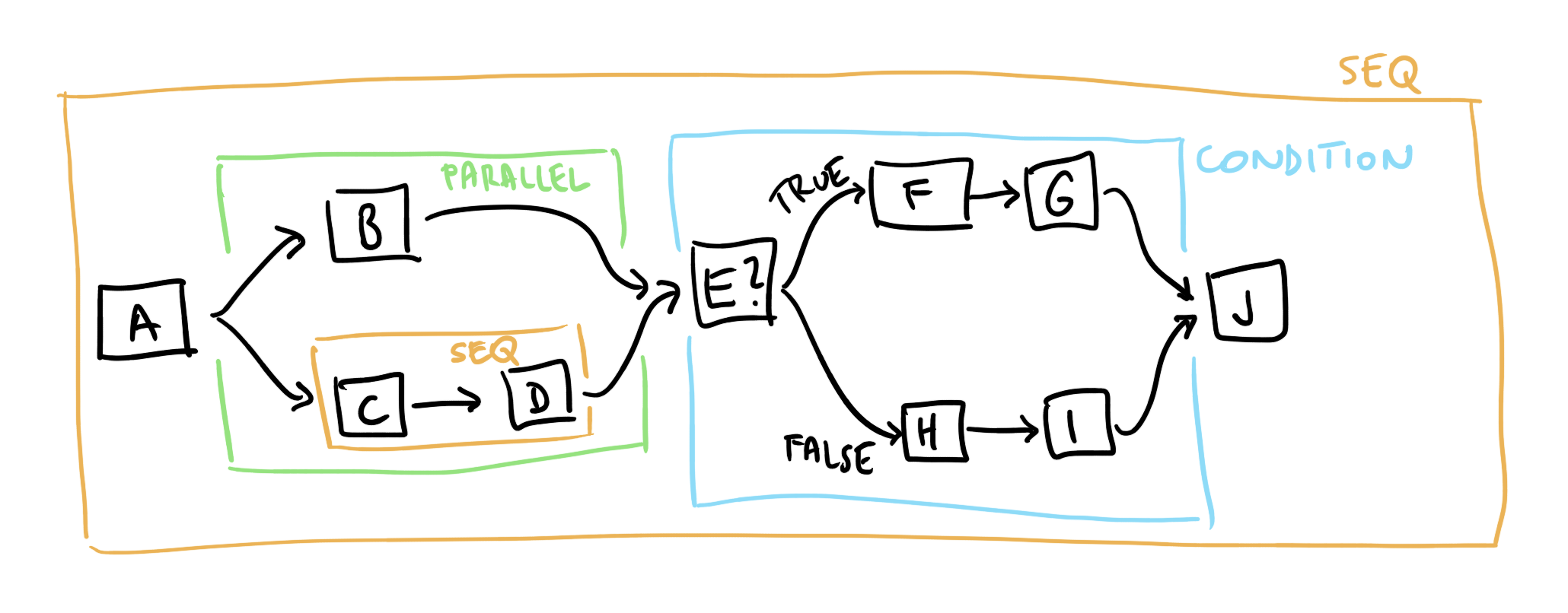
For example, a value
Sequence
[ Leaf "A"
, Parallel
[ Leaf "B"
, Sequence
[ Leaf "C"
, Leaf "D"
]
]
, Condition "E"
{ trueSeq = [ Leaf "F", Leaf "G" ]
, falseSeq = [ Leaf "H", Leaf "I" ]
}
, Leaf "J"
]
represents this Job workflow:
The function to list all values of a Job will have this type signature:
values : Job a -> List (a, List Step)
And we want it to produce output like this:
values
(Parallel
[ Sequence [ Leaf 1, Leaf 2 ]
, Leaf 3
, Condition 4
{ trueSeq = [ Leaf 5 ]
, falseSeq = [ Parallel [ Leaf 6, Leaf 7 ]]
}
]
)
-->
[ ( 1, [ InParallel 0, InSequence 0 ] )
, ( 2, [ InParallel 0, InSequence 1 ] )
, ( 3, [ InParallel 1 ] )
, ( 4, [ InParallel 2 ] )
, ( 5, [ InParallel 2, InCondTrue 0 ] )
, ( 6, [ InParallel 2, InCondFalse 0, InParallel 0 ] )
, ( 7, [ InParallel 2, InCondFalse 0, InParallel 1 ] )
]
Without further ado, here’s the implementation using our “make a TODO list and process it one-by-one” pattern:
type alias Todo = (Job a, List Step)
type alias Acc = List (a, List Step)
type alias Output = List (a, List Step)
values : Job a -> List (a, List Step)
values rootJob =
let
go : List Todo -> Acc -> Output
go todos acc =
case todos of
[] ->
-- We're finished!
-- Return the items found so far (and fix the order)
List.reverse acc
(job, revPath) :: rest ->
case job of
Leaf a ->
-- No children to add as TODOs
-- But we have a new value to output
go rest ((a, List.reverse revPath) :: acc)
Sequence xs ->
-- No new values to output
-- But we have children to add as TODOs!
-- We need to compute a new path for each of them
let
newTodos : List (Job a, List Step)
newTodos =
List.indexedMap
(\i x -> (x, InSequence i :: revPath))
xs
in
go (newTodos ++ rest) acc
Parallel xs ->
-- same as in Sequence
let
newTodos : List (Job a, List Step)
newTodos =
List.indexedMap
(\i x -> (x, InParallel i :: revPath))
xs
in
go (newTodos ++ rest) acc
Condition a {trueSeq, falseSeq} ->
-- We have both a new value to output
-- and new TODOs to process
let
newTodos : List (Job a, List Step)
newTodos =
List.concat
[ List.indexedMap
(\i x -> (x, InCondTrue i :: revPath))
trueSeq
, List.indexedMap
(\i x -> (x, InCondFalse i :: revPath))
falseSeq
]
in
go
(newTodos ++ rest)
((a, List.reverse revPath) :: acc)
in
go [(rootJob, [])] []
The above code eventually goes through all the TODOs (walks the whole tree), so switching between depth-first and breadth-first (again, corresponding to stack and queue respectively, and to new ++ rest vs rest ++ new) wouldn’t affect performance drastically, but it would change the order of the returned list. For this problem depth-first traversal made the most sense.
The TODOs aren’t just the Job values themselves: we also need a path the Job was found at. In general the shape of the TODO will be specific to your problem - you’ll need enough information to later process the TODO.
You can also see there is a fair bit of List.reverse happening in the above example - that’s a common pattern. In Elm it’s performant to insert to (linked) Lists at the beginning, so we’re doing new :: acc instead of acc ++ [new]. This often results in reversed lists - then it’s just a matter of fixing them with one last List.reverse before returning them.
Note your problem might not care about order at all and thus you could skip reversing!
It’s instructive to see the execution of the values function, so let’s add a Debug.log:
-go todos acc =
+go todos acc =
+ let
+ _ = Debug.log "go" { todos = todos, acc = acc }
+ in
Running the function on a (smaller) example now yields this (with whitespace added for clarity):
values
(Sequence
[ Leaf 1
, Parallel [ Leaf 2, Leaf 3 ]
, Leaf 4
]
)
-->
go: { todos = [ ( Sequence [ Leaf 1
, Parallel [ Leaf 2, Leaf 3 ]
, Leaf 4
] -- a TODO node
, [] -- path leading to this node
)
]
, acc = [] -- `acc`umulator - the output we're building
}
go: { todos = [ ( Leaf 1, [ InSequence 0 ] )
, ( Parallel [ Leaf 2, Leaf 3 ], [ InSequence 1 ] )
, ( Leaf 4, [ InSequence 2 ] )
]
, acc = []
}
go: { todos = [ ( Parallel [ Leaf 2, Leaf 3 ], [ InSequence 1 ] )
, ( Leaf 4, [ InSequence 2 ] )
]
, acc = [ ( 1, [ InSequence 0 ] ) ]
}
go: { todos = [ ( Leaf 2, [ InParallel 0, InSequence 1 ] )
-- note the paths are in reverse ^
, ( Leaf 3, [ InParallel 1, InSequence 1 ] )
, ( Leaf 4, [ InSequence 2 ] )
]
, acc = [ ( 1, [ InSequence 0 ] ) ]
}
go: { todos = [ ( Leaf 3, [ InParallel 1, InSequence 1 ] )
, ( Leaf 4, [ InSequence 2 ] )
]
, acc = [ ( 2, [ InSequence 1, InParallel 0 ] )
-- we fix (reverse) them when adding them to `acc`
, ( 1, [ InSequence 0 ] )
-- `acc` is _also_ in reverse order (2 then 1)
-- we'll fix it when returning from the `go` function
]
}
go: { todos = [ ( Leaf 4, [ InSequence 2 ] ) ]
, acc = [ ( 3, [ InSequence 1, InParallel 1 ] )
, ( 2, [ InSequence 1, InParallel 0 ] )
, ( 1, [ InSequence 0 ] )
]
}
go: { todos = []
, acc = [ ( 4, [ InSequence 2 ] )
, ( 3, [ InSequence 1, InParallel 1 ] )
, ( 2, [ InSequence 1, InParallel 0 ] )
, ( 1, [ InSequence 0 ] )
]
}
-- we've ran out of TODOs - we're done!
[ ( 1, [ InSequence 0 ] )
, ( 2, [ InSequence 1, InParallel 0 ] )
, ( 3, [ InSequence 1, InParallel 1 ] )
, ( 4, [ InSequence 2 ] )
]
One cool thing to note is that it doesn’t matter how many children our tree nodes have: we’re not recursing on the top-level function, like values left ++ values right or List.concatMap values xs. That wouldn’t be tail-call safe and could overflow the stack in some extreme cases (deep or wide trees) - there would be just too many values functions running at the same time and waiting for each other to finish.
Instead of calling the function n times, we add n TODOs to the list. We’re making our own explicit stack in the todos argument, and we’re keeping the implicit “system” one flat.
When we return
go ...from inside thegofunction, the Elm compiler optimizes that to a JSwhileloop instead of a function call - this is called Tail-call Optimization; TCO for short.
Searches (stop early)
There’s an important “sub-genre” of problems that can be done with this general “list of TODOs” shape: searches.
These generally bail out early (as soon as they find a solution), but sometimes need to find a best solution, which then can also lead to exhausting all options.
This is how I first encountered the pattern - Advent of Code has a lot of maze-solving, Dijkstra’s algorithm, flood-fill, optimization problems and so on. If examining one path gives me three more possible paths to take, I just add them as new TODOs into my todos stack and then recurse, continuing on to the next TODO.
Example
Here’s an example of a find function that works on the Jobs and List Step paths from the previous example:
find : (a -> Bool) -> Job a -> Maybe (a, List Step)
with an intended usage:
find
(\str -> String.startsWith "W" str)
(Sequence
[ Leaf "Foo"
, Parallel [ Leaf "Waldo", Leaf "Bar" ]
, Leaf "Baz"
, Condition "What?"
{ trueSeq = [ Leaf "Yeah" ]
, falseSeq = [ Leaf "Nah" ]
}
]
)
-->
Just ( "Waldo", [ InSequence 1, InParallel 0 ] )
This perhaps might be accomplished in an ad-hoc way recursively: find pred job = case job of .... But this would again have the issue of blowing the stack on large inputs.
Let’s see how it would look using the above pattern of “making a TODO of this and dealing with it in a future iteration.”
find : (a -> Bool) -> Job a -> Maybe (a, List Step)
find pred rootJob =
let
go : List (Job a, List Step) -> Maybe (a, List Step)
go todos =
case todos of
[] ->
-- We didn't find any value that would fit the predicate
Nothing
(job, revPath) :: rest ->
case job of
Leaf a ->
-- A value - let's test it.
-- This is our chance to stop early.
if pred a then
-- Found it!
Just (a, List.reverse revPath)
else
-- Nevermind, let's continue with other TODOs
go rest
Sequence xs ->
-- We can't test any value here
-- But we make a bunch of _smaller_ TODOs from `xs`
let
newTodos : List (Job a, List Step)
newTodos =
List.indexedMap
(\i x -> (x, InSequence i :: revPath))
xs
in
go (newTodos ++ rest)
Parallel xs ->
let
newTodos : List (Job a, List Step)
newTodos =
List.indexedMap
(\i x -> (x, InParallel i :: revPath))
xs
in
go (newTodos ++ rest)
Condition a {trueSeq, falseSeq} ->
-- Another value - another opportunity to stop!
if pred a then
-- Found it!
Just (a, List.reverse revPath)
else
let
newTodos : List (Job a, List Step)
newTodos =
List.concat
[ List.indexedMap
(\i x -> (x, InCondTrue i :: revPath))
trueSeq
, List.indexedMap
(\i x -> (x, InCondFalse i :: revPath))
falseSeq
]
in
go (newTodos ++ rest)
in
go [(rootJob, [])]
You can see similarities with values, in particular a lot of the same path-building is present; I haven’t explored this further but perhaps it hints at a possible Path-aware fold function from which both find and values functions could be derived. Let’s leave that for another time though :)
Also, the go function only has the list of TODOs as an argument; we don’t need to accumulate any state on the side, as the output can be derived from the TODO alone.
Optimization detour: pruning
The above was searching for any value satisfying a predicate. There’s another subclass of search problems, and that’s searching for best value satisfying a predicate (finding a shortest path through a graph etc.).
In these problems you can usually prune the list of TODOs in some way to remove needless work: why process a TODO if you can determine it can’t be the best one? This usually looks like:
case todos of
todo :: rest ->
if hasAChance todo then
-- process it
else
-- skip it
go rest
but you can also List.filter the TODO list whenever you find a new maximum. (Tradeoffs!)
Optimization detour: priority queues
In these search problems depth-first versus breadth-first does make a difference (particularly when you’re searching for any solution and not the best one, DFS is much better than BFS), and there’s one more thing I want to briefly mention again: priority queues.
A priority queue is a collection that automatically sorts its contents according to some criteria, and is able to give you (and/or remove) its current “top” element efficiently.
This is useful for a few of these algorithms (notably Dijkstra’s), so if you’re implementing a search or path-finding algorithm, be on the lookout for the opportunity to use a better data structure for your todos than just the simple List.
If you can get a decent solution at the beginning, it will also synergize well with the above idea of pruning: you’ll be able to prune more paths and do less work!
I’ve had good experience with the fifth-postulate/priority-queue package. The code shape changes to something similar to this:
go : Priority Todo -> Output
go todos =
case PriorityQueue.head todos of
Nothing ->
-- all TODOs processed!
Just bestTodo ->
let
rest : Priority Todo
rest = PriorityQueue.tail todos
in
-- process it
Summary
That’s mostly all I wanted to say about the pattern! I hope the two examples gave you an idea of where it might be used.
The pattern is not limited to trees and works equally as well for searching graphs; I’d even say there it’s much more useful because you can’t use simple recursion that is available to you with trees.
Let me repeat the main points:
- Some problems allow you to convert your problem into a list of TODOs and a function that takes one TODO from the list and processes it (potentially adding more TODOs to the list).
- You can easily switch between depth-first and breadth-first traversal by changing how you add new TODOs to the list.
- It’s better to
::than to++; but if you::, make sure to decide whether you need toList.reverseat the end. - The shape of the inner tail-recursive function (
go) is very flexible: use different arguments to help process your TODOs efficiently.- eg. a list of visited nodes (to prune / skip processing future ones),
- a priority queue of TODOs instead of a List,
- possibly an accumulated output to return at the end,
- etc.
Overall the pattern is nothing groundbreaking or new - it’s simply a list you process sequentially, one item at a time, adding new items when needed.
The let go todos = ... in go [firstTodo] shape is specific to Elm or functional programming in general; in a procedural language you’d perhaps use a while loop and mutate a list of TODOs instead.
Nonetheless I’ve found it helpful to give the pattern a name, to make it a thing, a tool I can then consider when solving certain problems.
So, go forth and multiply make some TODOs!
Acknowledgements
Thanks to Ed Kelly for proofreading and suggesting improvements.